在数学的广阔天地里，排列组合作为离散数学的一个重要分支，以其独特的魅力和广泛的应用吸引着无数求知者的目光，当我们提及“三位数的排列有多少组”时，实际上是在探讨由0到9这十个数字中任意选取三个数字进行全排列的所有可能情况，这个问题不仅考验着我们对基本数学原理的理解，还激发了我们对数字世界无限可能的探索欲。

排列组合的基础概念

在深入探讨三位数的排列之前，我们先来回顾一下排列组合的基本概念，排列（Permutation）是指从n个不同元素中取出m（m≤n）个元素，按照一定的顺序进行排列的方式，而组合（Combination）则是指从n个不同元素中取出m个元素，不考虑元素的顺序，本篇文章聚焦于三位数的全排列，即m=3的情况。

三位数的排列分析

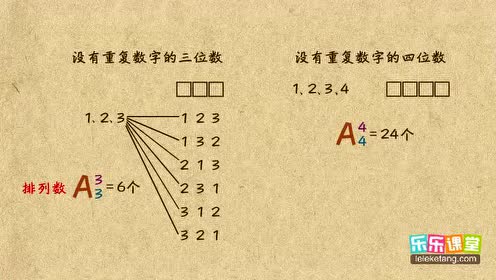
要计算三位数的所有可能排列，我们可以从最直观的“全或不全”原则出发：对于每一位上的数字，都有10种选择（0-9），但当我们将某一位上的数字选定后，下一位的选择就会减少一种（因为不能有重复的数字），最后一位则只剩下8种选择（除去前两位已选和0的情况），这种简单的分析忽略了0不能作为最高位数的规则（即百位上不能为0）。

考虑0的特殊情况：由于0不能作为百位，我们首先考虑不含0的三位数的排列，对于这种情况，每位数都可以从1到9中选择，共有9×9×8=648种排列方式，我们加上以0开头的三位数（即十位和个位从1到9中选择），这样的排列有9×9=81种（因为百位固定为0后，剩下的两位可以自由选择），但需注意，这里我们重复计算了“000”这一无效组合，因此需要减去1次。

综合计算：不含0的三位数有648种排列方式，以0开头的三位数（除去无效的“000”）有81-1=80种排列方式，总的三位数排列数为648 + 80 = 728种。

深入理解与实际应用

虽然通过上述计算我们得出了728这个具体数字，但这一过程背后所蕴含的数学逻辑和思想却是更为宝贵的收获，它不仅加深了我们对排列组合原理的理解，还展示了数学在解决实际问题中的强大能力，在密码学、编码学、彩票抽奖等领域，对数字排列的掌握能够设计出更加安全或有趣的规则，在物流、交通管理等领域，通过对车辆号牌、航班号等的编排规则设计，也能有效减少混淆和错误的发生。

拓展思考：四位数的排列

既然我们已经掌握了三位数排列的奥秘，那么对于四位数的排列又该如何思考呢？同样地，我们可以先不考虑前导零的情况（即首位不能为0），则有9×9×9×8=5832种排列方式；再考虑以0开头的情形（除去“0000”），即9×9×8=648种，四位数总共有5832 + 648 = 6480种不同的排列方式，这一过程不仅加深了我们对数学规律的认识，也体现了数学递归思想的魅力。

通过对“三位数的排列有多少组”这一问题的探讨，我们不仅得到了一个具体的答案——728种不同的排列方式，更重要的是在这个过程中学习了排列组合的基本原理、应用了数学逻辑进行问题分解与解决的方法，数学不仅仅是公式和定理的堆砌，它更是一种思维方式、一种探索未知世界的工具，在未来的学习与生活中，掌握好这些基础而重要的数学概念和技能，将有助于我们更好地理解世界、解决问题、创造价值。